The wide availability of user-provided content in online social media facilitates the aggregation of people around common interests, worldviews, and narratives.
However, the World Wide Web is a fruitful environment for the massive diffusion of unverified rumors.
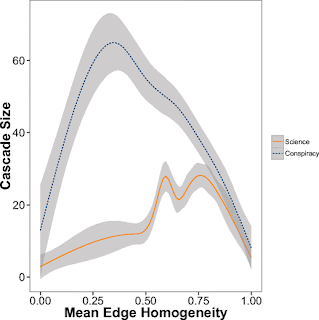
In this work, using a massive quantitative analysis of Facebook, we show that information related to distinct narratives––conspiracy theories and scientific news––generates homogeneous and polarized communities (i.e., echo chambers) having similar information consumption patterns. Then, we derive a data-driven percolation model of rumor spreading that demonstrates that homogeneity and polarization are the main determinants for predicting cascades’ size.
We find that, although consumers of scientific and conspiracy stories present similar consumption patterns with respect to content, cascade dynamics differ. Selective exposure to content is the primary driver of content diffusion and generates the formation of homogeneous clusters, i.e., “echo chambers.”
Anatomy of Cascades.
misinformation virality Facebook rumor spreading cascades
The massive diffusion of sociotechnical systems and microblogging platforms on the World Wide Web (WWW) creates a direct path from producers to consumers of content, i.e., allows disintermediation, and changes the way users become informed, debate, and form their opinions
Homogeneous Clusters.
This disintermediated environment can foster confusion about causation, and thus encourage speculation, rumors, and mistrust
we provide important insights toward the understanding of the mechanism behind rumor spreading. Our findings show that users mostly tend to select and share content related to a specific narrative and to ignore the rest. In particular, we show that social homogeneity is the primary driver of content diffusion, and one frequent result is the formation of homogeneous, polarized clusters. Most of the times the information is taken by a friend having the same profile (polarization)––i.e., belonging to the same echo chamber.
Users tend to aggregate in communities of interest, which causes reinforcement and fosters confirmation bias, segregation, and polarization. This comes at the expense of the quality of the information and leads to proliferation of biased narratives fomented by unsubstantiated rumors, mistrust, and paranoia.
According to these settings algorithmic solutions do not seem to be the best options in breaking such a symmetry. Next envisioned steps of our research are to study efficient communication strategies accounting for social and cognitive determinants behind massive digital misinformation.
Our findings show that users mostly tend to select and share content according to a specific narrative and to ignore the rest. This suggests that the determinant for the formation of echo chambers is confirmation bias. To model this mechanism we now introduce a percolation model of rumor spreading to account for homogeneity and polarization. We consider n users connected by a small-world network (41) with rewiring probability r. Every node has an opinion ωiωi, i∈{1,n}i∈{1,n} uniformly distributed between [0,1][0,1] and is exposed to m news items with a content ϑj,j∈{1,m}ϑj, j∈{1,m} uniformly distributed in [0,1][0,1]. At each step the news items are diffused and initially shared by a group of first sharers. After the first step, the news recursively passes to the neighborhoods of previous step sharers, e.g., those of the first sharers during the second step. If a friend of the previous step sharers has an opinion close to the fitness of the news, then she shares the news again.
When
∣∣ωi−ϑj∣∣≤δ,
|ωi−ϑj|≤δ,
user i shares news j; δ is the sharing threshold.
Because δ by itself cannot capture the homogeneous clusters observed in the data, we model the connectivity pattern as a signed network (4, 42) considering different fractions of homogeneous links and hence restricting diffusion of news only to homogeneous links. We define ϕHLϕHL as the fraction of homogeneous links in the network, M as the number of total links, and nhnh as the number of homogeneous links; thus, we have
ϕHL=nhM,0≤nh≤M.
ϕHL=nhM, 0≤nh≤M.
Notice that 0≤ϕHL≤10≤ϕHL≤1 and that 1−ϕHL1−ϕHL, the fraction of nonhomogeneous links, is complementary to ϕHLϕHL. In particular, we can reduce the parameters space to ϕHL∈[0.5,1]ϕHL∈[0.5,1] as we would restrict our attention to either one of the two complementary clusters.
The model can be seen as a branching process where the sharing threshold δ and neighborhood dimension z are the key parameters. More formally, let the fitness θjθj of the jth news and the opinion ωiωi of a the ith user be uniformly independent identically distributed (i.i.d.) between [0,1][0,1]. Then the probability p that a user i shares a post j is defined by a probability
p=min(1,θ+δ)−max(0,θ−δ)≈2δ
p=min(1,θ+δ)−max(0,θ−δ)≈2δ,
because θ and ω are uniformly i.i.d. In general, if ω and θ have distributions f(ω)f(ω) and f(θ)f(θ), then p will depend on θ,
pθ=f(θ)∫max(0,θ−δ)min(1,θ+δ)f(ω)dω.
pθ=f(θ)∫max(0,θ−δ)min(1,θ+δ)f(ω)dω.
If we are on a tree of degree z (or on a sparse lattice of degree z+1z+1), the average number of sharers (the branching ratio) is defined by
μ=zp≈2δz,
μ=zp≈2δ z,
with a critical cascade size S=(1−μ)−1S=(1−μ)−1. If we assume that the distribution of the number m of the first sharers is f(m)f(m), then the average cascade size is
S=∑mf(m)m(1−μ)−1=⟨m⟩f1−μ≈⟨m⟩f1−2δz,
S=∑mf(m)m(1−μ)−1=〈m〉f1−μ≈〈m〉f1−2δz,
where ⟨…⟩f=∑m…f(m)〈…〉f=∑m…f(m) is the average with respect to f.
In the simulations we fixed neighborhood dimension z=8z=8 because the branching ratio μ depends upon the product of z and δ and, without loss of generality, we can consider the variation of just one of them.
If we allow a probability q that a neighbor of a user has a different polarization, then the branching ratio becomes μ=z(1−q)pμ=z(1−q)p. If a lattice has a degree distribution d(k)d(k) (k=z+1k=z+1), we can then assume a usual percolation process that provides a critical branching ratio and that is linear in ⟨k2⟩d/⟨k⟩d〈k2〉d/〈k〉d (μ≈(1−q)p⟨z2⟩/⟨z⟩μ≈(1−q)p〈z2〉/〈z〉).
0 comments:
Post a Comment